Introduction to support vector machines

Support vector machines, which were a de facto standard in machine learning until the end of the first decade of the 21st century, were eclipsed by neural networks, longer-lived techniques, however, the increase in computing power of the computers of the new century and, above all, with the emergence of convolutional neural networks, they once again became the hegemonic technology.

The No Free Lunch Theorem states that no algorithm consistently yields the best results for all problems. For this reason, a priori, it cannot be determined that one algorithm is better than another in a given problem. For this, there are certain types of problems in which an SVM will perform better than deep learning techniques.

Support vector machines are found within machine learning in a field called supervised machine learning. This means that the algorithm is trained with certain previously labeled input data, so that, later, it can give an output label to new data based on the patterns recognized in the input.

What are SVMs

They are maximum margin classifiers using the kernel trick to project the training data samples into a higher-dimensional space, making them linearly separable (or nearly separable).

Let’s borrow a great explanation of SVMs for dummies:

We have balls of two colors (red and blue) on a table that we want to separate or classify.

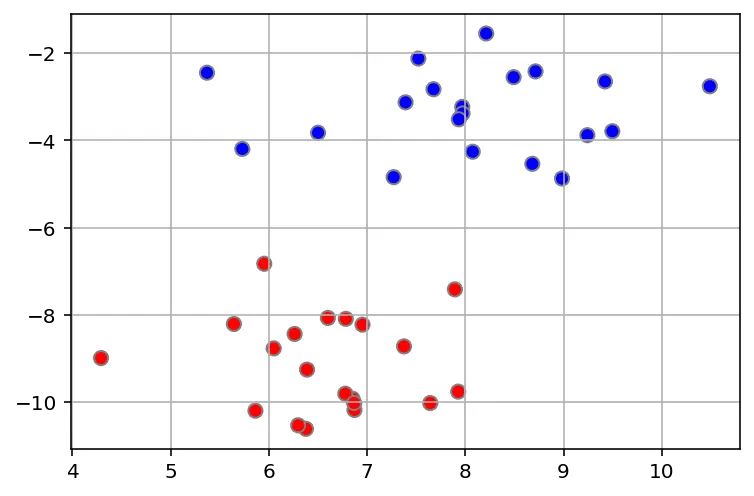
We can just get a stick and put it on the table, this works pretty well right? The problem is that we can place the stick in several ways separating the balls. If we introduce a new uncolored ball (green mark), and we want to assign it a color, we will assign it depending on the chosen stick.

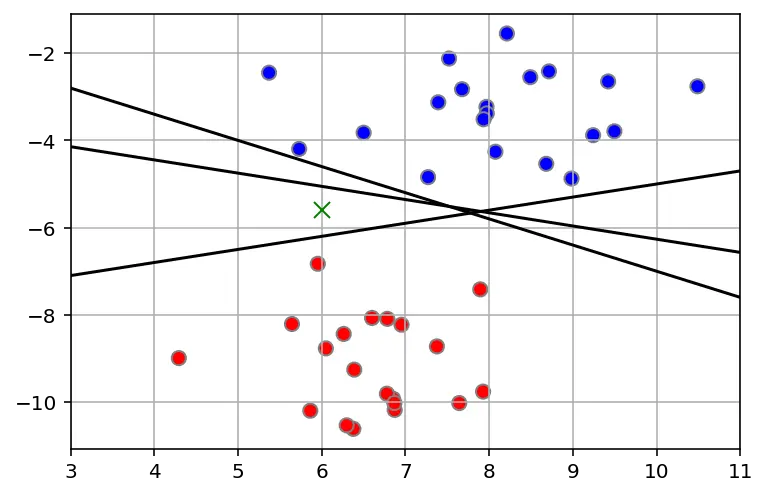
So, what is the best position of the stick? Well, the one that maximizes the margin between balls. This ensures that the color of the ball is the one of the closest group. Being the probability of belonging to a said class (color) higher. This is called the maximal margin classifier.

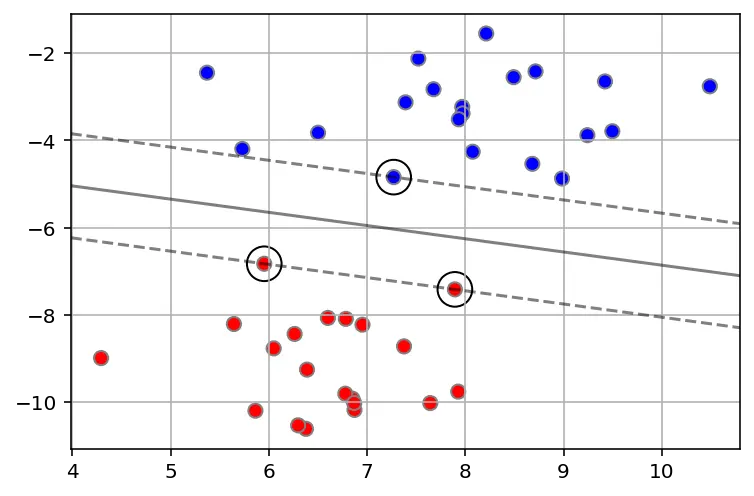
Now, some villain comes and places more balls on the table in a way such that no stick in the world will let you split those balls well.

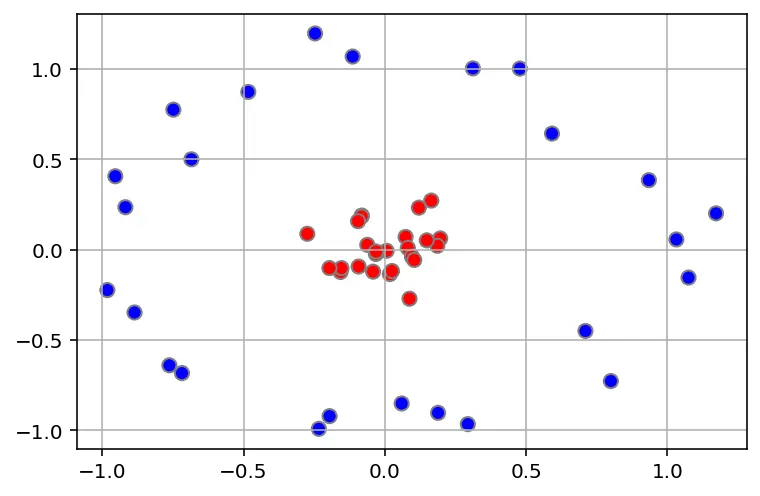
So what do you do? You flip the table of course! Throwing the balls into the air. Then, with your pro ninja skills, you grab a sheet of paper and slip it between the balls.

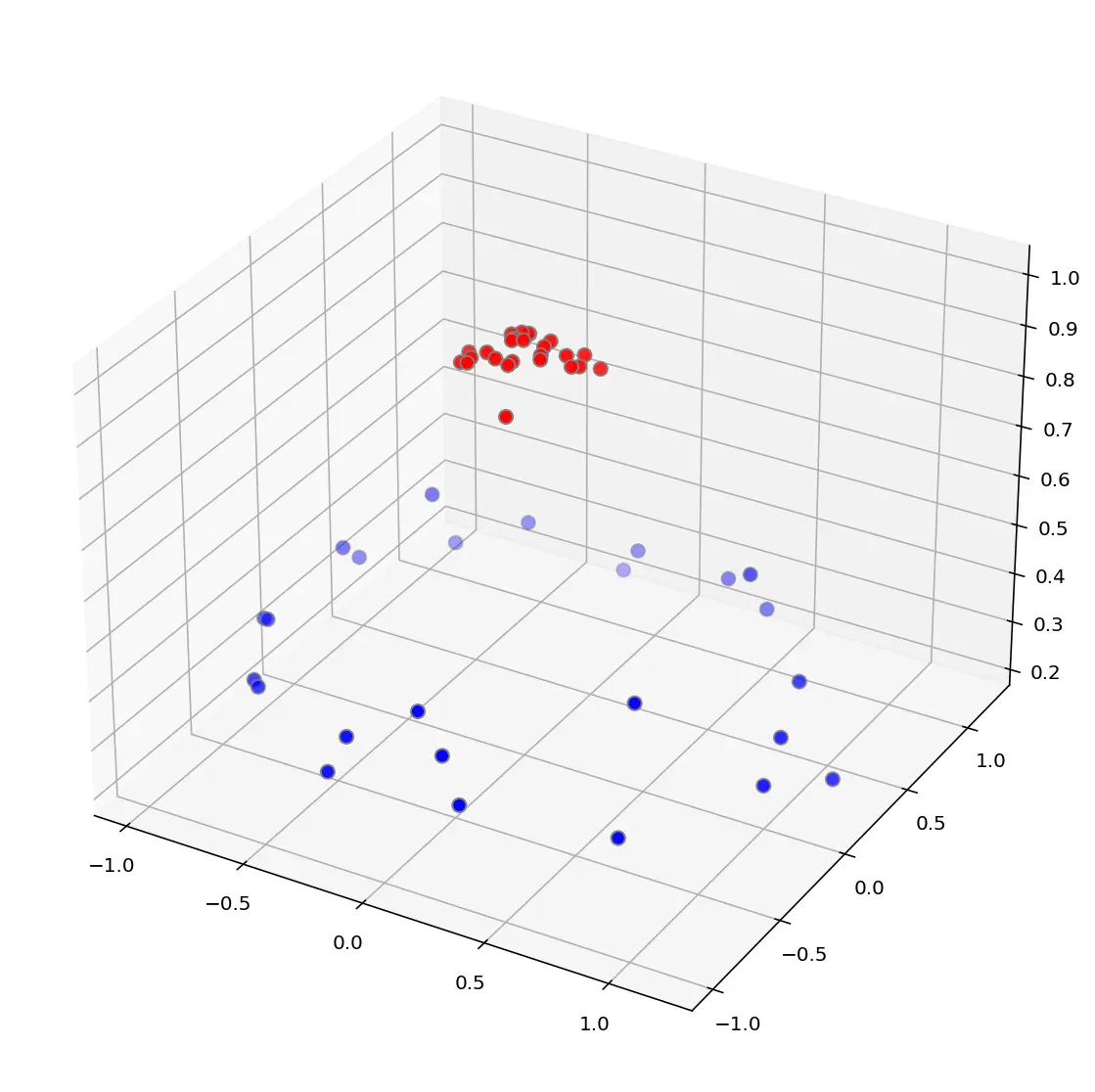
Now, looking at the balls from where the villain is standing, they balls will look split by some curvy line.

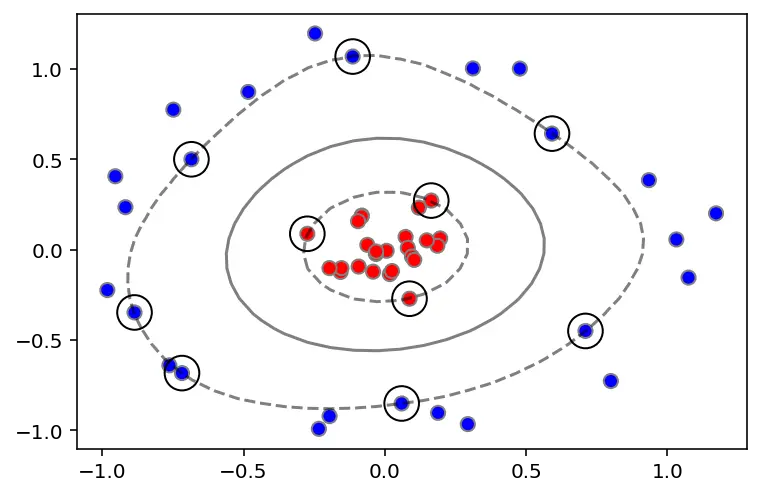
Boring adults the call balls data, the colors classes, the stick a classifier, the biggest gap trick optimization, call flipping the table kernelling, the piece of paper a hyperplane, and the balls on the margins, support vectors.